Since: Jun./06th/2004
暗号学は数学の 1 分野です。主に軍事利用の観点で発展してきました。歴史的に使われた有名な暗号に、帝政ローマ時代に使われたとされる、ジュリアス・シーザーのシーザー暗 号、アメリカ南北戦争時代に使われたビジネル暗号、第二次大戦中に使われた、日本軍のパープル暗号、ドイツのエニグマ暗号などが挙げられます。
シーザー暗号 (Caesar Ciphers) は、アルファベットを前後に何文字かずらした単純換字暗号です。復号化して平文に戻すための鍵は、ずらす文字数になります。例えば、IBM を 1 文字前にシフト（又は 25 回シフト）すると HAL になります。偶然って、あんた、そんな上手い話しがありますかいな・・・
ビジネル暗号 (Vegenere Ciphers) は、多表式換字暗号です。アルファベットをシフトして並べた 25 × 25 のマトリックスの縦横に、平文と鍵語を対応させ、交差する地点の文字に換字します。例えば、マトリックスを作るときのアルファベットのシフトを 1 文字として、平文を SUGAI、鍵語 MANABU とすれば、暗号文は EUTAJ となります。
エニグマ暗号 (Enigma Ciphers) やパープル暗号（97式欧文印字機）は、暗号機と呼ばれる機械を使った精巧な換字暗号です。入力文字は、内部の複数枚の歯車の組み合わせと、背面のプラグ の接続を経て、暗号化されます。鍵は、歯車の組み合わせ方とプラグの接続方法です。
エニグマの場合は、最終的には、6 枚の歯車のうち 4 枚が変更可能で、プラグはアルファベット 26 文字の中から任意の 10 組の文字間を接続するものとなったそうです。この場合の鍵の個数は、およそ 10 20 個以上になり、現在の暗号アルゴリズムよりも多いくらいです。エニグマの動作原理については、上山清二氏のページに詳しい説明があります。
歴史的な暗号は、その殆どが換字暗号です。これに、文字を入れ替える転置暗号 (Transposition Ciphers) を組み合わせるなどして、暗号の強度を高めていました。
現代的な暗号は、文字符号化方法に基づいています。文字符号化方法 (Character Encodings)は、二進数のテーブルに文字をマップするものです。
文字符号化に基づく現代的な暗号は、その形式によって、ストリーム暗号とブロック暗号に分けられます。
符号化したビット列を、一ビットずつ変換する方法をストリーム暗号と呼びます。
ビットに対しては、0/1 の何れかしかないので、反転させる／反転しないの二種類の演算しかありません。最も単純な場合は、平文 "h" 0x111000 に対して、
鍵語 0x010101 で、1を反転／0を反転しないとすれば、
暗号文 "=" 0x101101 が得られることになります。この関係は、排他論理和 (XOR) になっており、111000 ⊕ 010101 = 101101 となります。
符号化したビット列を、一定のブロックに区切って暗号化する方法をブロック暗号と呼びます。ブロッキングの方法で、次の四つに分けられます：
M2 ⊕ C1 を暗号化して得られます。結果として、ある暗号文ブロック Mn は、それまでの全てのブロック M1 ～ Mn-1 に依存することになります。
 |
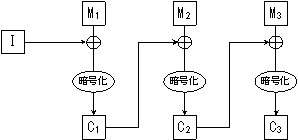| 図：CBC の概念図 |
|---|
Cn = Mn ⊕ EK(Cn-1) となります。
 |
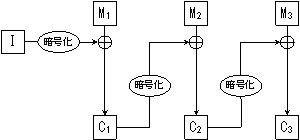| 図：CFB の概念図 |
|---|
C1 = EK(M1 ⊕ I) を得ることがあります。CFB の場合、ブロック間の連鎖を目的とせず、暗号文ブロックは、初期値を繰り返し暗号化して排他論理和の項として、Cn = Mn ⊕ EK(In-1) として与えられます。
 |
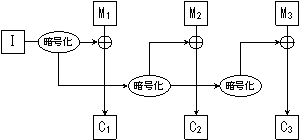| 図：OFB の概念図 |
|---|
ストリーム暗号／ブロック暗号は、平文のビット列を暗号化する単位の区別でした。鍵の管理方法に基づいて、対称鍵暗号（秘密鍵暗号）と非対称鍵暗号（公開鍵暗号）に分けることもできます。
対称鍵暗号方式は秘密鍵暗号方式（共通鍵暗号方式）とも呼ばれます。
一つの鍵で、暗号化と復号化を行います。復号化は暗号化の逆の操作になります。通信文の受け手と送り手は、第三者に鍵を秘密にすることで、盗聴による漏洩／改竄を防ぎます。対称鍵暗号方式の鍵のことを秘密鍵 (secret key) と呼びます。
DES は "Data Encyption Standard" の意味です。IBM が開発した Lucipher を元に、 USA の連邦情報処理標準 が 1977 年に発行した FIPS PUB 46-2 (Federal Information Processing Standards 46-2) として採用されています。
AES は "Advanced Encyption Standard" の意味です。USA の連邦情報処理標準 (FIPS PUB 197, Federal Information Processing Standards 197) として採用されています。
1970 年代に策定された DES から 30 年が経過し、総当り攻撃 (Brute Force Attack) が現実味を帯びる中で、DES に代わる新しい標準として策定されたものです。DES では 256 個の鍵の個数が最大です。これを総当り攻撃で解読するには、専用マシン (Deep Crack) で 4, 5 日あれば十分だという話です。
公開鍵暗号方式は非対称鍵暗号方式とも呼ばれます。
暗号化鍵と復号化鍵に、別の鍵を用います。通信文の送り手は、プライベートな秘密の暗号化鍵で暗号化します。暗号文の受け手は、公開された復号化鍵 で平文に復号化します。秘密の暗号化鍵を秘密鍵 (private key) と呼び、公開された復号化鍵を公開鍵 (public key) と呼びます。
RSA は、Rivest-Rivest-Shamir-Adleman による、米国マサチューセッツ州 RSA Security 社の開発した暗号です。
DSA は、"Digital Signature Algorithm" の意味です。USA の連邦情報処理標準 (FICS PUB 186-2, Federal Information Processing Standards 186-2) では、電子署名アルゴリズムとして、DSA, RSA, Elliptic Curve DSA を採用しています。
ECC は "Elliptic Curve Cryptography" の意味です。楕円曲線暗号と訳します。色々な規格がありますが、ECDSA (Elliptic Curve DSA) が有名です。DSA の項で挙げた、 USA の連邦情報処理標準 (FICS PUB 186-2, Federal Information Processing Standards 186-2) にて、電子署名アルゴリズムとして、DSA, RSA と共に Elliptic Curve DSA (ECDSA) が採用されています。
暗号化は、平文を暗号化して暗号文を生成して、暗号文を復号化して平文を得るためのものです。しかし、平文から復号化できない暗号文を生成すること が有意義なケースがあります。復号化出来ない暗号文を生成する関数を一方向関数 (one-way function) と呼びます。
1 方向関数とは、入力に演算して出力を求めるもので、逆の演算ができないもののことを言います。入力 x, 出力 y, 両者の関係 y = f(x) であるとき、x = f-1(y) が得られない f(x) を指します。f-1 のことを、函数（関数） f の逆函数（インバース）と呼びます。
メッセージのダイジェストに 1 方向関数を演算することで得られたハッシュ値は、メッセージが改竄されていないことを保障するためのデジタル署名（電子署名）に使われます。電子署名 (electronic signature) は、電子指紋 (degital finger-print) とも呼ばれます。
メッセージとデジタル署名を別々に送ることで、メッセージの受け手は、メッセージに 1 方向関数を演算して得られたハッシュ値と署名を比較することで、メッセージが署名された時点のものから改竄されていないことを確認できます。メッセージと 署名が同時に改竄されていれば、メッセージの受け手は、それを見破る術はありません。
メッセージ・ダイジェストを得るためのアルゴリズムの一つです。RFC1321 で規定されています。MD4 が破られたことにより策定されました。FIPS 準拠ではありません。
MD5 関数には非常に微妙な規則性が発見されたので、現在では SHA1 を使うことが主流になっています。Verisine のサーバ認証も、MD5 から SHA1 に変更されています。
SHA-1 は "Secure Hash Algorithm 1" を意味です。RFC3174 で規定されています。USA の連邦情報処理標準 (FIPS PUB 180-1, Federal Information Processing Standards 180-1) として採用されており、電子署名で支配的な標準です。メッセージダイジェストを生成するハッシュ関数に SHA-1 を用い、それを暗号化して証明書に署名するために DSA を採用することが標準的な選択となります。