算術演算の Tips and Tricks

Revised: Feb./7th/2005; Since: Feb./23rd/2003

コンピュータのことを計算機と呼ぶことがあります。科学技術計算の現場では「計算機を回す」と言いますし、企業や研究施設の「電算センター」、「計算機室」という名称にその名残があります。現在の分散系システムでは通信機能の方が注目される傾向にありますが、計算は今でもコンピュータの重要な仕事です。コンピュータ上では、限られた桁の2進数に対して、ビット反転を組み合わせることで四則演算を表現するので、特有の問題が生じることもあります。ここではJavaでの数値表現について紹介します。

プリミティブ型とラッパー・クラスの違いは？

数値、ブール代数、文字を表現するデータは、ラッパー・クラスと呼ばれる参照型のオブジェクトでも表現できます。しかし、これはオブジェクト生成を含むコストの高い方法です。

基本的なデータには参照型でない（オブジェクトでない）データ型が用意されています。プリミティブ型と呼ばれるこれらのデータ型には、対応するクラスも用意されており、ラッパー・クラスと呼ばれます。ラッパー・クラスは、プリミティブ型データを格納する不変オブジェクトを生成します（表1）。

表1. プリミティブ型と対応するラッパー・クラス
意味	プリミティブ型	ラッパー・クラス
8ビット符号付整数	byte	java.lang.Byte
16ビット符号付整数	short	java.lang.Short
32ビット符号付整数	int	java.lang.Integer
64ビット符号付整数	long	java.lang.Long
16ビットUNICODE（文字）	char	java.lang.Character
32ビット符号付浮動小数点数	float	java.lang.Float
64ビット符号付浮動小数点数	double	java.lang.Double
ブール代数（真偽値）	boolean	java.lang.Boolean

Javaアプリケーションは、メモリ上の、スタックとヒープと呼ばれる領域で実行されます。プリミティブ型データはスタックに格納されます。オブジェクトは、インスタンス（メソッドや型、及びデータ）がヒープに格納され、そのポインタがスタックに格納されます。ラッパー・クラス型オブジェクトより、プリミティブ型の方がメモリ・コストもパフォーマンスも良くなります。ラッパー・クラスでなければならない事情として、次のことが挙げられます：

ラッパー・クラスのメソッドを使いたい。
VectorなどのAPIに入出力したい。

他のクラスのメソッドから、オブジェクトが要求されているなど、止むを得ないとき以外は、ラッパー・クラスを使わない方が良いでしょう。

浮動小数点の比較は危険？

コンピュータは内部的には二進数で表現して演算しています。つまり、小数の場合は、1/2 + 1/2² + 1/2³ + 1/2⁴ という形式で表現しています。十進数で考えた場合と、殆ど、概ね、正確に変換できますが、ほんのわずかだけ異なることがあります。

例えば、0.1の10倍は1です。float型でもdouble型でも同じです。しかし、0.1を10回足しても、わずかに1に足りません！例えば、0.1を2進数で表現すると次のようになります。

100110011001100110011001100110011001100110011001...

これを2の累乗の分数で表現すると、次のようになります。

1/10 = 1/16 + 1/32 + 1/256 + 1/512 + 1/4096 + 1/8192 + ...

つまり、無限級数となってしまい、厳密な値を求めるためには、無限に演算する必要があります。そのため、途中で計算を打ち切ることになり、微小な誤差が生まれます。厳密な値との誤差を打切り誤差と呼びます。一般に、算術計算では切り捨て／四捨五入／切り上げが必要になることが殆どで、そのために生じる誤差を丸め誤差と呼びます。

よって、浮動小数点数同士を比較するときは、比較対照の絶対値に対して十分に大きな差による大小比較は安全ですが、== による等しいことの判断は危険です。簡単な計算の結果、等しくなるつもりでも、演算順序や値の受け取り方によって誤差が生じ、== の評価結果が変わってしまう可能性があるからです。

class FloatDemo {
	public static void main(String[] args) {
		// 同じ値になるはず
		double d1 = 1.0 - 0.9;
		double d2 = 1.0/10.0;
		// 比較
		System.out.println(d1 == d2);
		// プリント
		System.out.println(d1);
		System.out.println(d2);
		// 16進数表現
		System.out.println(Long.toHexString(Double.doubleToLongBits(d1)));
		System.out.println(Long.toHexString(Double.doubleToLongBits(d2)));
	}
}

>javac FloatDemo.java

>java FloatDemo
false
0.09999999999999998
0.1
3fb9999999999998
3fb999999999999a

浮動小数点数には、他にも、NaN（非数）やInfinity（無限）などがあるため、取り扱いに注意が必要がことがあります。可能であれば、浮動小数点同士の比較は避けた方が無難です。一般には、次のような回避策が挙げられます。

10のn乗を掛けて整数にする
クラスBigDecimalなどのラッパーを使う
丸め誤差が出ないようにする。（乗除算の順番を変えるなど）
出ても影響しないくらい大きく比較する（相対誤差で有為な値を求めるなど）

もっと厳密に計算できる？

浮動小数点に関する誤差は、二進数と十進数の差に起因するもので、BigDecimalクラスを使うことで回避できます。

一般に、算術計算時には様々な誤差が発生します。古くから計算機の計算結果を正しく評価する試みが続けられてきました。注意が必要な代表的な誤差には次のものがあります。

オーバーフロー／アンダーフロー（桁あふれ）: 大き過ぎたり小さ過ぎたりする数値が、表現できる桁からはみ出ること
丸め誤差: 無限小数などを有効桁内に収めるための、切り捨て／四捨五入／切り上げなどによって生じる誤差
打切り誤差: 無限に演算する必要があるものを、有限回数で打ち切ることによって生じる誤差
桁落ち: 絶対値が微小な差しかない数値間での加減算で、結果が有効数字の桁より小さいために、無意味な出力が得られること
情報落ち: 絶対値の大きな数と小さな数の間の加減算で、有効数値の桁より小さい数値が計算結果に含まれないために、出力が無意味となること

　金融やECサイトなどの勘定系と呼ばれる金融計算システムでは、このような誤差を許容できません。これらの問題を回避するために、以下のような方法が使われます。

掛け算と割り算の順番を入れ替える
相対誤差を計算する
10を何回か掛けて整数化する

java.mathパッケージのBigIntegerやBigDecimalは、これらの問題を解決する一つの方法です。

BigIntegerとBigDecimalは、Stringやラッパー・クラスと同様、不変オブジェクトです。BigIntegerは任意精度の整数を表現することができます。BigDecimalは任意精度の符号付小数点数を取り扱え、丸め誤差を制御できます。BigIntegerは他にも素数や基数の問題を解決するために使えるのですが、ここではより利用頻度の高いBigDecimalを紹介します。

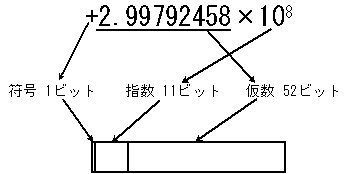
Javaのプリミティブ型では、浮動小数点数はIEEE 754規格の2進数で表現されます。これは要するに、小数を2のn乗の級数で表現する方法の一つであり、float型の32ビットや倍精度のdouble型64ビットを、何のために何ビット使うかを指定したものです（図1）。

図1. IEEE 754規格倍精度浮動小数点数（数値は光速度[m/s]）

double型符号付浮動小数点数の64ビットを使えば、日常の感覚では極めて精密な数値をコンパクトに表現できます。しかし、例えば0.1が厳密に表現できないのです。というのも、2進数では、小数をという、の級数で表現するため、0.1を表現すると、1/10 = 1/16 + 1/32 + 1/256 + 1/512 + 1/4096 + 1/8192 + …という無限小数になってしまうために、打切り誤差が発生します。

BigDecimalを使えば、任意精度の小数を厳密に表現できます。指定した精度の桁数内で、厳密な結果を保証し、計算時に丸めモードを定数として指定することで、丸め誤差を制御できます（表2）。

表2. BigDecimalクラスで丸めモードを指定する定数
定数	説明
ROUND_CEILING	正の無限大に近づくように丸めます
ROUND_DOWN	0に近づけるように丸めます
ROUND_FLOOR	負の無限大に近づくように丸めます
ROUND_HALF_DOWN	「もっとも近い数字」に丸めます。両隣の数字が等距離の場合は切り捨てます。
ROUND_HALF_EVEN	「もっとも近い数字」に丸めます。両隣の数字が等距離の場合は偶数側に丸めます。
ROUND_HALF_UP	「もっとも近い数字」に丸めます。両隣の数字が等距離の場合は切り上げます。
ROUND_UNNECESSARY	十分な桁数が用意できて、丸める必要がない場合に指定します。
ROUND_UP	0から離れるように丸めます

BigDecimalでは四則演算をメソッドで実行します。例えば、BigDecimalの値aを同じくbで割るとき、丸めモードをROUND_DOWNで実行する場合は次のようになります。

// a/bの実行
a.divide(b, BigDecimal.ROUND_DOWN);

有効数字の指定は簡単で、コンストラクタに与える引数の桁数で揃えられます。例えば、リスト1を見てみましょう。ここでは、rateが0.250、掛け算対象のunitは1で初期化しています。一方が小点数以下3桁、一方が0桁なので、この場合の計算結果は小点数以下3桁で出力されます。この結果にもう一度unitを掛けると、両方とも3桁になりますので、結果は6桁になります。以下、乗算の都度3桁ずつ増えていき、無限に桁が出力されることになります。

▼リスト1

// java.math.BigDecimal の import
import java.math.*;
class BigDecimalDemo {
    public static void main(String[] args) {
        // インスタンス化
        BigDecimal rate = new BigDecimal("0.250");
        BigDecimal unit = new BigDecimal("1");
    	
        for (int i = 0; i < 10; i++) {
            // BigInteger 型オブジェクトの乗算
            unit = unit.multiply(rate);
        	System.out.println(unit);
        }
    }
}

リスト1の実行結果は次のようになります。

0.250
0.062500
0.015625000
0.003906250000
0.000976562500000
0.000244140625000000
0.000061035156250000000
0.000015258789062500000000
0.000003814697265625000000000
0.000000953674316406250000000000

桁数を指定できることは便利なのですが、逆に言うと、この桁数の指定が足りないと、ROUND_HALF_DOWNなどでばっさりと数字が落とされるので、無意味な結果が得られることもあります。そのため、設計の時点で、有効数字が何桁あれば良いのか、計算結果が何桁になるのかを正しく把握しておくことが重要です。

プリミティブ型ではサイズが小さい、精度が低い、丸め誤差が許容できないという場合には、BigInteger、BigDecimalの利用を検討します。但し、不変オブジェクトであることに起因する、オブジェクトの生成とコピーの繰り返しが発生します。そのため、サイズも計算速度もプリミティブ型よりも格段に悪化します。パフォーマンスと精度のトレードオフであることを理解した上で使ってください。

数値のフォーマットは指定できる？

BigDecimalなどで結果が厳密なことは良いことなのですが、帳票印刷などで出力枠の桁数が決まっている場合には、そのままでは使えません。このようなときは、java.text.NumberFormatとそのサブクラスであるjava.text.DecimalFormatを使ってみましょう。

リスト2は年間の利子0.000300から月ごとの利子を計算し、12ヵ月分の残高を計算したものです。月利を算出するときに丸め誤差をROUND_HALF_DOWNで計算しています。何も指定しなければ、計算するごとに6桁ずつ増えていくはずですが、それでは非常に不恰好です。ここではフォーマットを指定して、利率はx.xxxx%、残高は￥x,xxxと出力されるようにしています。

残高では、getCurrencyInstance()メソッドによって、実行コンピュータのロケールから貨幣の出力フォーマットを取得しています。一方、%の出力では、DecimalFormatクラスを使って、自分でフォーマットを指定しています。

▼リスト2

// java.math.BigDecimal の import
import java.math.*;
// java.text.NumberFormatとjava.text.DecimalFormat の import
import java.text.*;
class BigDecimalDemo2 {
    public static void main(String[] args) {
    // インスタンス化
    BigDecimal rate = new BigDecimal("0.000300");
    BigDecimal MONTH = new BigDecimal("12");
        BigDecimal balance = new BigDecimal(100000000);
    // 丸めモード ROUND_HALF_DOWN を指定した除算
    BigDecimal monthlyRate = rate.divide(MONTH, BigDecimal.ROUND_HALF_DOWN);
        
        // 小数点以下4桁のフォーマットを指定
        NumberFormat nf = new DecimalFormat("0.0000%");
        
        // BigDecimal値をdoubleに変換し、フォーマットを適用
        System.out.println("年利: " + nf.format(rate.doubleValue()));
        System.out.println("月利: " + nf.format(monthlyRate.doubleValue()));
        // 当該コンピュータのロケールに応じた通貨単位のフォーマットを指定
        nf = NumberFormat.getCurrencyInstance();
        for (int i=0; i < 12; i++) {
            // 乗算
            BigDecimal interest = balance.multiply(monthlyRate);
            // 加算
            balance = balance.add(interest);
            // BigDecimalをdouble値に変換し、フォーマットを適用
            System.out.println("残高: " + nf.format(balance.doubleValue()));
        }
    }
}

リスト2の実行結果は次のようになります。

年利: 0.0300%
月利: 0.0025%
残高: ￥100,002,500
残高: ￥100,005,000
残高: ￥100,007,500
残高: ￥100,010,000
残高: ￥100,012,501
残高: ￥100,015,001
残高: ￥100,017,501
残高: ￥100,020,002
残高: ￥100,022,502
残高: ￥100,025,003
残高: ￥100,027,503
残高: ￥100,030,004

ロケールなどで既存のフォーマットが利用できるときはNumberFormat、単位などを独自にカスタマイズしたい場合はDecimalFormatを使いましょう。